What Is an IQ?
Originally, intelligence testing was used to detect children of lower intelligence in order to place them in special education programs. The first IQ tests were designed to compare a child’s intelligence to what his or her intelligence “should be” as compared to the child’s age. If the child was significantly smarter than a normal child of his or her age, the child was given a higher score, and if the child scored lower than expected for a child of his or her age, the child was given a lower IQ score.
This method of determining mental age doesn’t work too well when testing adults, and today, we attempt to write tests that will determine an person’s true mental potential, unbiased by culture, and compare their scores to the scores of others who have taken the same test.
So, we compare a person’s objective results to the objective results of other people, and determine how intelligent each test taker is compared to all other test takers, instead of comparing test takers to an arbitrary age related standard.
Standard Deviation
The first step to understanding IQ testing is to understand standard deviation.
To understand this concept, it can help to learn about what statisticians call normal distribution of data.
A normal distribution of data means that most of the examples in a set of data are close to the average, while relatively few examples tend to one extreme or the other.
Let’s say you are writing a story about nutrition. You need to look at people’s typical daily calorie consumption. Like most data, the numbers for people’s typical consumption probably will turn out to be normally distributed. That is, for most people, their consumption will be close to the mean, while fewer people eat a lot more or a lot less than the mean.
When you think about it, that’s just common sense. Not that many people are getting by on a single serving of kelp and rice. Or on eight meals of steak and milkshakes. Most people lie somewhere in between.
If you looked at normally distributed data on a graph, it would look something like this:

The x-axis (the horizontal one) is the value in question–calories consumed, dollars earned or crimes committed, for example. And the y-axis (the vertical one) is the number of datapoints for each value on the x-axis–the number of people who eat x calories, the number of households that earn x dollars, or the number of cities with x crimes committed.
Now, not all sets of data will have graphs that look this perfect. Some will have relatively flat curves, others will be pretty steep. Sometimes the mean will lean a little bit to one side or the other. But all normally distributed data will have something like this same “bell curve” shape.
The standard deviation is a statistic that tells you how tightly all the various examples are clustered around the mean in a set of data. When the examples are pretty tightly bunched together and the bell-shaped curve is steep, the standard deviation is small. When the examples are spread apart and the bell curve is relatively flat, that tells you you have a relatively large standard deviation.
Computing the value of a standard deviation is complicated, but let me show you graphically what a standard deviation represents.
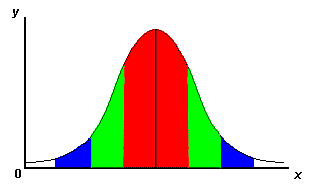
One standard deviation away from the mean in either direction on the horizontal axis (the red area on the above graph) accounts for about 68 percent of the people in this group. Two standard deviations away from the mean (the red and green areas) account for roughly 95 percent of the people. And three standard deviations (the red, green and blue areas) account for about 99 percent of the people.
If this curve were flatter and more spread out, the standard deviation would have to be larger in order to account for those 68 percent or so of the people. So that’s why the standard deviation can tell you how spread out the examples in a set are from the mean.
Why is this useful? Here’s an example: If you are comparing test scores for different schools, the standard deviation will tell you how diverse the test scores are for each school.
Let’s say School A has a higher mean test score than School B. Your first reaction might be to say that the kids at School A are smarter.
But a bigger standard deviation for one school tells you that there are relatively more kids at that school scoring toward one extreme or the other. By asking a few follow-up questions you might find that, say, School A’s mean was skewed up because the school district sends all of the gifted kids to School A. Or that School B’s scores were dragged down because students who recently have been “mainstreamed” from special education classes have all been sent to School B.
In this way, looking at the standard deviation can help point you in the right direction when asking why data is the way it is.
The standard deviation can also help you evaluate the worth of all those so-called “studies” that seem to be released to the press everyday. A large standard deviation in a study that claims to show a relationship between eating cupcakes and winning marathons, for example, might tip you off that the study’s claims aren’t all that trustworthy.
Here is one formula for computing the standard deviation.
A warning, this is for math geeks only! Those seeking only a basic understanding of stats don’t need to read any further. Remember, a decent calculator and stats program will calculate this for you.
Terms you’ll need to know
x = one value in your set of data
(x) = the mean (average) of all values x in your set of data
n = the number of values x in your set of data
For each value x, subtract (x) from x, then multiply that value by itself (otherwise known as determining the square of that value). Sum up all those squared values. Then multiply that value by this value: 1/(n-1). Then take the square root of the resulting value. That’s the standard deviation of your set of data.
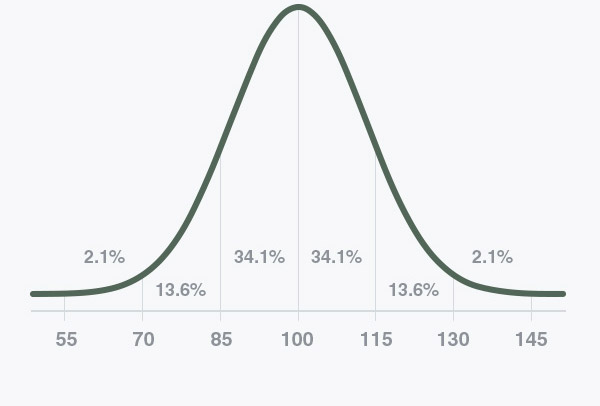
The standard deviation of the test at IQTest.com is 15. That means that each one of the bars in the graph above represents a span of 15 points. So, 68% of testers will have scores between 85 and 115, or within one standard deviation of the mean. 95% of testers will have scores between 70 and 130, or within two standard deviations of the mean. And 99% of testers will have scores between 55 and 145, or within 3 standard deviations of the mean. A score four standard deviations from the mean is very rare. Less than 1% of testers score in the fourth standard deviation above or below the mean.
The bell curve shown on the homepage illustrates a standard deviation of 15.
Defining Intelligence
Most people have an intuitive notion of what intelligence is, and many words in the English language distinguish between different levels of intellectual skill: bright/dull, smart/stupid, clever/slow, and so on. Yet no universally accepted definition of intelligence exists, and people continue to debate what, exactly, it is. Fundamental questions remain: Is intelligence one general ability or several independent systems of abilities? Is intelligence a property of the brain, a characteristic of behavior, or a set of knowledge and skills?
The simplest definition proposed is that intelligence is whatever intelligence tests measure. But this definition does not characterize the ability well, and it has several problems. First, it is circular: The tests are assumed to verify the existence of intelligence, which in turn is measurable by the tests. Second, many different intelligence tests exist, and they do not all measure the same thing. In fact, the makers of the first intelligence tests did not begin with a precise idea of what they wanted to measure. Finally, the definition says very little about the specific nature of intelligence.
Whenever scientists are asked to define intelligence in terms of what causes it or what it actually is, almost every scientist comes up with a different definition. For example, in 1921 an academic journal asked 14 prominent psychologists and educators to define intelligence. The journal received 14 different definitions, although many experts emphasized the ability to learn from experience and the ability to adapt to one’s environment. In 1986 researchers repeated the experiment by asking 25 experts for their definition of intelligence. The researchers received many different definitions: general adaptability to new problems in life; ability to engage in abstract thinking; adjustment to the environment; capacity for knowledge and knowledge possessed; general capacity for independence, originality, and productiveness in thinking; capacity to acquire capacity; apprehension of relevant relationships; ability to judge, to understand, and to reason; deduction of relationships; and innate, general cognitive ability.
People in the general population have somewhat different conceptions of intelligence than do most experts. Laypersons and the popular press tend to emphasize cleverness, common sense, practical problem solving ability, verbal ability, and interest in learning. In addition, many people think social competence is an important component of intelligence.
Most intelligence researchers define intelligence as what is measured by intelligence tests, but some scholars argue that this definition is inadequate and that intelligence is whatever abilities are valued by one’s culture. According to this perspective, conceptions of intelligence vary from culture to culture. For example, North Americans often associate verbal and mathematical skills with intelligence, but some seafaring cultures in the islands of the South Pacific view spatial memory and navigational skills as markers of intelligence. Those who believe intelligence is culturally relative dispute the idea that any one test could fairly measure intelligence across different cultures. Others, however, view intelligence as a basic cognitive ability independent of culture.
In recent years, a number of theorists have argued that standard intelligence tests measure only a portion of the human abilities that could be considered aspects of intelligence. Other scholars believe that such tests accurately measure intelligence and that the lack of agreement on a definition of intelligence does not invalidate its measurement. In their view, intelligence is much like many scientific concepts that are accurately measured well before scientists understand what the measurement actually means. Gravity, temperature, and radiation are all examples of concepts that were measured before they were understood.
Take the Test at IQTest.com now
____________________________________________